[Union-Find 알고리즘 이해 (합 집합 찾기)]
- 원소들의 연결 여부를 확인하며, 부모가 더 작은 원소를 부모로 삼도록 함
- 대표적인 그래프 알고리즘으로 합집합 찾기라는 의미를 가짐
- 여러 노드가 존재할 때, 두 개의 노드를 선택해서 현재 노드가 서로 같은 그래프에 속하는지 판별
[Union-Find 알고리즘 방식 ]
<각자 자신을 원소로 가짐>
서로 원소들을 연결할 때 같은 값을 가리키도록 하며,
처음에는 아무런 원소도 연결되어 있지 않으므로 모든 값이 자기 자신을 가리키도록 한다.
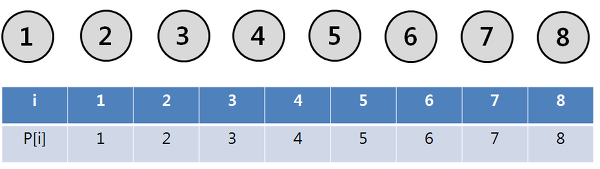
P는 Parent(부모 노드)를 뜻하며 원소가 어떤 부모를 가리키는지 나타낸다.
P[i] = i 로 나타낼 수 있으며 이 방식으로 같은 부모 노드를 가진 원소들의 집합도 얻을 수 있다.
[1- 4 노드를 합칠 경우 ]
1과 4의 부모 노드가 같게 해야 하는데, 더 작은 노드를 부모 노드로 삼기로 했으므로 P[4]를 1로 변경한다.
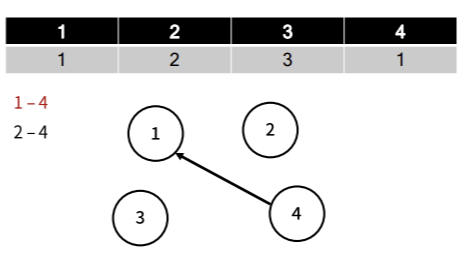
[2- 4 노드를 합칠 경우 ]
2와 4의 부모 노드를 같게 해야한다.
2의 부모 노드는 2, 4의 부모 노드는 1이므로 더 작은 노드를 부모로 삼기 위해서
4의 부모 노드인 1에 접근한다.
1의 부모 노드는 1이므로 2의 부모 노드 역시 1이 된다.
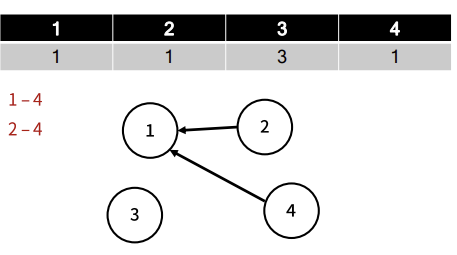
이로써 1- 2 -4 노드가 합집합이 되었다.
{1, 2, 4} , {3} 두 집합으로 나누어졌다.
2와 4를 합칠 때 2는 4의 부모 노드로 접근한다.
또 4는 1의 부모 노드로 접근한다.
마지막으로 1은 부모 노드가 자신이므로 더 이상 접근할 수 없다.
재귀적 탐색을 진행해서 부모 노드가 자기 자신일 경우까지 탐색을 한다.
그 이후에 부모 노드의 값을 합칠 노드의 값으로 설정하면 합 집합이 완성된다.
[Python 코드로 확인하기]
2가지 함수가 필요하다.
1. find(x) : 재귀적 탐색을 통해서 최 상위 부모의 값을 찾아낸다.
def find(x):
if x == parent[x]:
return x
else:
p = find(parent[x])
parent[x] = p
return parent[x]
2. union(x, y) : 각 최 상위 부모의 값을 찾은 후에 더 작은 값의 최상위 부모 값을 합칠 노드의 부모 값으로 설정한다.
def union(x, y):
x = find(x) #최상위 합집합으로 이동
y = find(y) #최상위 합집합으로 이동
# 같으면 이미 합집합
if x != y:
parent[y] = x
여기서 최상위 부모 값이 같은 경우는 이미 합집합인 경우이므로 진행하지 않는다.
자기 자신을 부모 값으로 가지는 딕셔너리를 선언한 후에 find, union 함수를 통해서 합 집합을 진행한다.
parent = []
for i in range(0,5):
parent.append(i)
union(1,4)
union(2,4)
for i in range(1, len(parent)):
print(find(i), end=' ')
각 최상위 부모 값을 출력했는데 결과는 1 1 3 1이 된다.
만약에 3번 노드까지 1, 2, 4번 노드 중 하나와 union을 진행한다면,
각 노드의 최상의 노드로 이동한 후에 3번 노드의 부모 값인 3을 1로 변경해준다.
결과는 {1,2,3,4}가 하나의 집합이 되고 각 부모 값은 1 1 1 1이 된다.
시간 복잡도를 줄여주며, 집합을 합치는데 매우 유용한 알고리즘인 것 같다.

