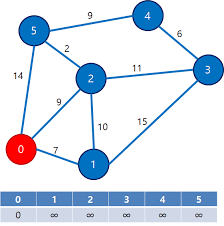
다익스트라 알고리즘
다익스트라 알고리즘은 최단거리를 구하는 알고리즘입니다.
다익스트라 알고리즘을 사용하면, 하나의 노드로부터 최단 거리에 있는 다른 노드를 탐색할 수 있습니다.
목적지와 가중치를 저장하여 가장 적은 가중치의 경로를 탐색할 수 있으며, 지하철 노선 탐색을 예로 들 수 있습니다.
최단 거리를 구할 노드로부터 거리가 입력된 노드를 돌아가면서 더 거리가 짧은 값이 나오면 값을 새로 갱신합니다.
알고리즘 구성
각 노드까지의 거리를 최대값으로 초기화하고, 해당 노드로 이동할 수 있는 더 작은 값일 나올 때 값을 갱신합니다.
INF = 1e8
distance = [INF] * (n+1)
INF는 정수의 최대값이며, 1~n까지의 거리값을 저장하기 위해서 n+1로 초기화합니다.
다음으로는 도착 노드와 가중치 값을 저장할 graph를 선언합니다.
graph = [[] for _ in range(n+1)] # 1번 ~ n번 노드
for _ in range(m):
u,v,w = map(int,input().split()) # 각 출발, 도착, 가중치
graph[u].append((v,w)) # 목적지, 가중치 입력
출발지로부터 여러개의 도착지가 있을수도 잇으므로 리스트로 관리합니다.
각 그래프의 인덱스를 출발지로 생각하고 (도착지, 가중치(v,w)) 를 저장합니다.
나중에 그래프에 저장된 도착지 별 가중치를 초기화하며 가장 적은 값을 찾을 수 있습니다.
다익스트라 알고리즘 탐색
알고리즘을 적용시키기 위해서 그래프와 목적지별 가중치를 생성했습니다. (graph, distance)
이제 다익스트라 알고리즘을 구현해서 탐색을 진행할 수 있습니다.
import heapq
다익스트라 알고리즘은 일반적으로 heapq를 사용합니다.
각 큐에 저장 된 데이터를 pop하면서 적은 값부터 순서대로 데이터를 탐색할 수 있습니다.
def dijkstra(start):
q = []
heapq.heappush(q,(start,0)) # 자기 자신이 목적지인 경우 가중치 0
distance[start] = 0
start로 탐색을 시작할 값을 지정합니다.
자기 자신으로 이동할 수 없으므로 start의 가중치는 0으로 초기화합니다.
다음 탐색을 위해서 q 리스트에 heapq를 활용해서 연결된 노드들을 확인합니다.
while문을 돌면서 첫 노드에서 연결된 모든 노드를 확인해서 가중치를 갱신하고, 다음 노드로 탐색을 진행하는 과정을 반복합니다.
def dijkstra(start):
q = []
heapq.heappush(q,(start,0)) # 자기 자신이 목적지인 경우 가중치 0
distance[start] = 0
while q:
now, dist = heapq.heappop(q)
if distance[now] < dist: # 이미 입력 값이 현재 노드 거리보다 더 작다면 생략
continue
for i in graph[now]: # 모든 연결 노드 탐색
if dist + i[1] < distance[i[0]]: # 기존 입력 값이 크면 교체
# i[0] -> 목적지, i[1] -> 가중치
distance[i[0]] = dist + i[1]
heapq.heappush(q,(i[0],dist+i[1]))
출발지 k를 통해서 각 목적지에 대한 가중치를 알 수 있습니다.
distance의 인덱스 탐색을 통해서 도착지에 대한 가중치를 얻을 수 있습니다.
dijkstra(k)
print(graph)
print(distance)
아래의 입력값으로 그래프를 구성하는 경우 distance에 1로부터 각 노드로의 가중치가 저장됩니다.
5 6
1
5 1 1
1 2 1
1 3 3
2 3 1
2 4 5
3 4 2
[[], [(2, 1), (3, 3)], [(3, 1), (4, 5)], [(4, 2)], [], [(1, 1)]]
[100000000.0, 0, 1, 2, 4, 100000000.0]
0번 인덱스와 5번 인덱스의 값은 해당 인덱스로 가는 경로가 없기 때문에 INF 값이 들어있는 것을 볼 수 있습니다.
실제 문제에 적용하기
백준 1446번 지름길 문제를 풀면서 해당 알고리즘을 적용해 보았습니다.
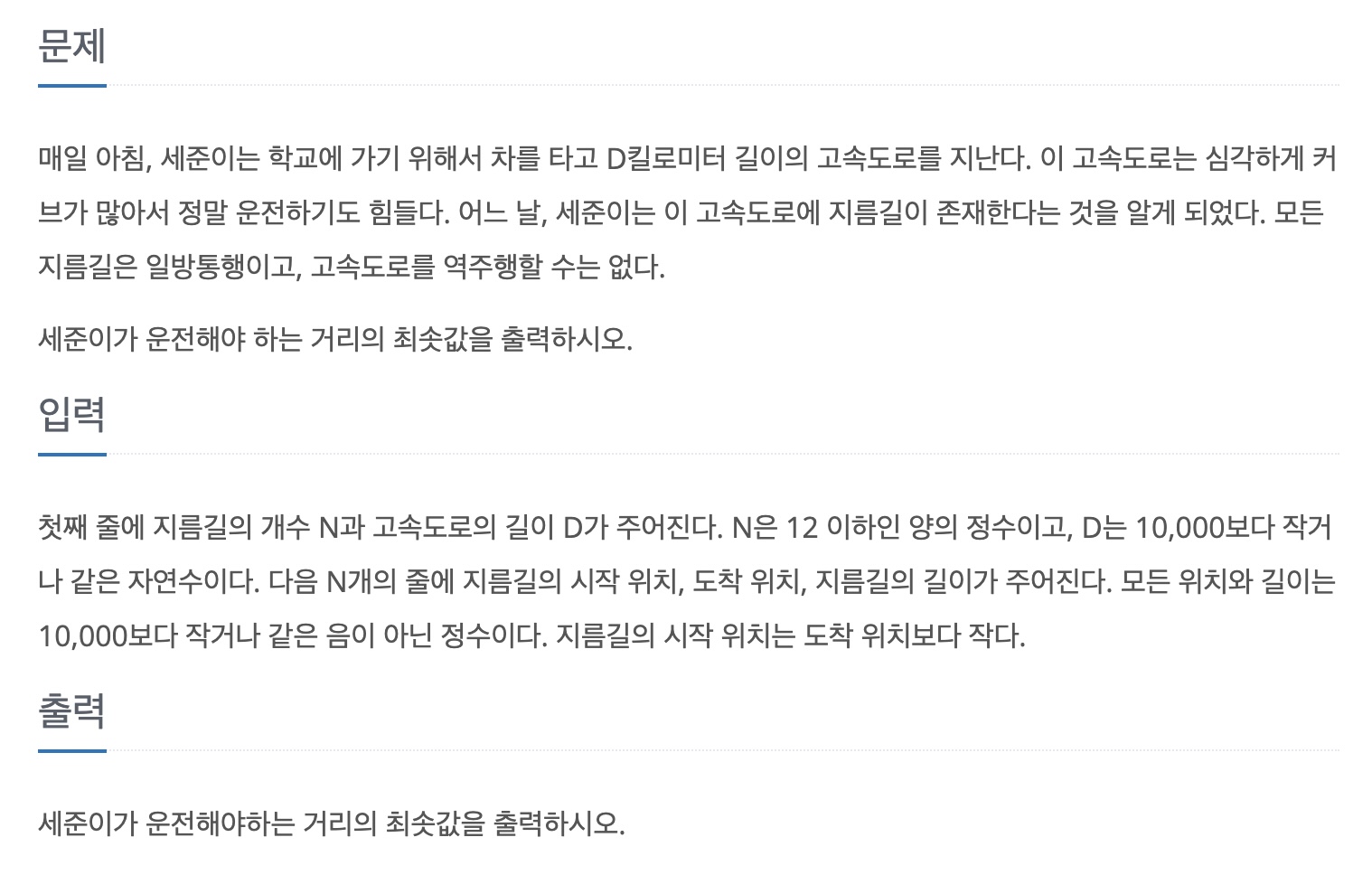
해당 문제에서는 다익스트라 알고리즘을 활용하는 것을 요구하고 있습니다.
세준이의 지름길 활용에 다익스트라 알고리즘을 적용하며, 목적지까지 가능 과정을 킬로미터 당 하나의 노드로 봤습니다.
## 지름길
import heapq
n,d = list(map(int,input().split()))
INF = 1e8
graph = [[] for i in range(d+1)]
for i in range(d):
graph[i].append((i+1,1))
distance = [INF] * (d+1)
for _ in range(n):
u,v,w = map(int,input().split()) # v는 목적지, w는 가중치
if v> d: continue # 목적지가 더 큰 경우 제외
graph[u].append((v,w))
def dijkstra():
q = []
heapq.heappush(q,(0,0))
distance[0] = 0
while q:
now, dist = heapq.heappop(q)
if distance[now] < dist:
continue
for i in graph[now]:
new_w = dist + i[1]
# distance[i[0]] : prev w
if new_w < distance[i[0]]:
distance[i[0]] = new_w
heapq.heappush(q,(i[0],new_w))
dijkstra()
print(distance[d])
추가 된 코드가 있다면, 목적지가 더 큰 경우를 제외하는 것인데요.
고속도로에서 뒤로 갈 수 없다고 명시되어 있으므로 목적지를 넘어가는 v값이 입력되었을 경우 저장하지 않습니다.
q를 탐색하면서 기존에 저장 된 값보다 더 큰값이 dist로 나올 경우 탐색을 진행하지 않으면서 시간복잡도를 감소시킬 수 있었습니다.

