Array(List)의 특징과 장단점
Array 배열을 활용하면 순차적으로 데이터를 저장한다는 특징이 있습니다.
데이터에 순서가 있기 때문에 0부터 시작하는 index가 존재하며, index를 사용해 특정 요소를 찾고 수정이 가능합니다.
순차적으로 존재하는 데이터의 중간에 요소가 삽입되거나 삭제되는 경우 그 뒤의 모든 요소들이 한 칸씩 뒤로 밀리게 됩니다.
순서가 중요한 자료구조에서 순서를 보장해주는 Array를 활용하는 것이 좋습니다.
Kotlin에서의 Array와 List
array는 사이즈가 할당되어져 있고, Mutable 타입이므로 수정이 가능합니다.
인덱스를 참조해서 값을 수정할 수 있다는 장점이 있습니다.
리스트는 순서가 있고, 사이즈는 자동할당되며 대부분 수정이 불가능한 ImmutableList 타입입니다.
Array와 다르게 인덱스로 값을 수정할 수 없으며, ArrayList로 선언해야 값을 수정할 수 있습니다.
ArrayList를 활용하는 경우, 크기를 리사이징 하기 때문에 성능이 저하된다는 단점이 있습니다.
Stack과 Queue
스택과 큐는 선형 자료구조이며, Array와 LinkedList를 통해 구현할 수 있습니다.
스택은 후입선출(LIFO) 방식으로 나중에 들어간 원소가 먼저 나오는 구조입니다.
자바의 스택 메모리 영역에서 스택 자료구조가 활용되게 됩니다.
지역변수와 매개변수 데이터 값이 저장되는 공간이며, 메소드 호출 시 메모리에 할당되고 종료되면 메모리가 해제됩니다.
큐는 선입선출(FIFO) 방식으로 먼저 들어간 원소가 먼저 나오는 구조를 가집니다.
자원의 할당과 회수를 하는 스케줄러가 대표적인 큐의 역할이라고 볼 수 있습니다.
메모리에 적재된 다수의 프로세스 중 어떤 프로세스에게 자원을 할당할 것인가 그 순서를 결정하는 것이
자원이 효율적인 사용에 있고, 선입선처리를 활용하여 큐를 적용시킨 방식입니다.
우선순위 큐는 들어간 순서에 상관없이 우선순위가 높은 데이터를 먼저 꺼내기 위해 고안된 자료구조 입니다.
배열, 연결 리스트, 힙 등이 있고, 힙 방식이 시간 복잡도를 보장하기 때문에 보통 완전 이진트리 형태의 힙을 활용합니다.
코틀린에서의 Stack
class StackStructure {
private val stack = arrayListOf<Int>()
fun push(item: Int){
assert(stack.size< MAX_STACK_SIZE){
stack.add(item)
}
}
fun pop(){
assert(stack.size > MIN_STACK_SIZE){
stack.removeLast()
}
}
fun printStacks(){
stack.forEach{
println(it)
}
}
companion object {
const val MAX_STACK_SIZE = 10
const val MIN_STACK_SIZE = 0
}
}
코틀린 코드로 위와 같이 스택을 구현할 수 있으며, 아래와 같이 자체적으로 구현된 스택을 활용할 수 있습니다.
private val stack = Stack<Int>()
구현 된 스택 클래스에서 push, pop 등의 기본적인 스택 함수를 편리하게 사용할 수 있습니다.
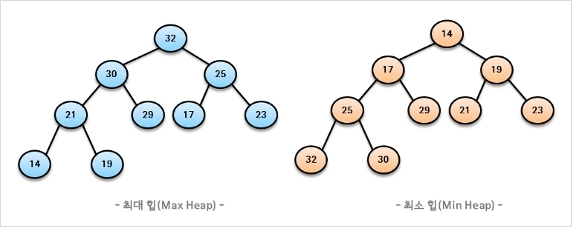
Tree와 Heap 구조
Tree는 스택과 큐와 같은 선형 구조가 아닌 비선형 자료구조이며, 계층적 관계를 표현하는데 사용합니다.
Heap은 최댓값 또는 최솟값을 찾아내는 연산을 쉽게 하기 위해 고안된 구조로,
각 노드의 키 값이 자식의 키값보다 작지 않거나(최대힙 구성), 그 자식의 키 값보다 크지 않는(최소힙 구성) 완전 이진 트리입니다.
Array와 LinkedList 비교
Array는 index를 활용해 해당 원소에 접근할 수 있습니다.
찾고자 하는 원소의 인덱스 값을 알고 있으면 해당 원소로 쉽게 접근할 수 있으며, 속도가 빠르다는 장점이 있습니다.
이러한 방식을 RandomAccess라고 하며, 쉬운 방법으로 접근이 가능합니다.
하지만 삽입과 삭제 과정에서 각 원소들을 shift 해줘야 하는 비용이 생겨 시간 복잡도 O(n)이 발생합니다.

이 문제를 해결하기 위해서 LinkedList가 등장하였습니다.
각각의 원소들은 자기 자신 다음에 어떤 원소인지만을 기억하고 있기 때문에 이 부분만 다른 값으로 바꿔서 해결할 수 있습니다.
하지만 LinkedList는 원하는 위치에 한 번에 접근하기 어렵다는 단점이 있습니다.
원하는 위치에 삽입을 하고자 하면 원하는 위치에 도달하기 위해서 첫 번째 원소부터 탐색해야 합니다.
해시 테이블
해시 테이블은 Key, Value로 데이터를 저장하는 자료구조 중 하나로 빠르게 데이터를 검색할 수 있습니다.
내부적으로 배열을 사용하여 데이터를 저장하는 방식으로 빠른 검색 속도를 제공합니다.
각 key값은 해시함수에 의해 고유한 index를 가지게 되어 바로 접근할 수 있으므로 평균 O(1)의 시간 복잡도를 가집니다.
하지만 index값이 충돌한 경우 연결된 리스트들까지 검색해야 하므로 O(N)까지 시간 복잡도가 증가할 수 있습니다.
Hash Map과 Hash Table
동기화 지원 여부와 null 값 허용 여부에 차이가 있습니다.
해시 테이블은 null 값을 허용하지 않기 때문에 병렬 처리를 할 때 Thread-safe 하다는 장점이 있습니다.
반면에 해시 맵은 null 값을 허용하며, Thread-safe하지 않다는 단점이 있습니다.
BST(Binary Search Tree) : 이진 탐색 트리
이진 트리(Binary Tree)는 자식 노드가 최대 두 개인 노드들로 구성 된 트리이고,
이진 탐색 트리(Binary Search Tree)는 이진 탐색과 연결 리스트를 결합한 자료구조입니다.

이진 탐색의 효율적인 탐색 능력을 유지하면서, 이진 탐색의 단점인 자료 입력과 삭제를 장점으로 가지고 있습니다.
이를 통해서 이진 트리와, 연결 리스트의 장점을 모두 활용할 수 있습니다.
이진 탐색 트리는 왼쪽 트리의 모든 값이 반드시 부모 노드보다 작아야 하고, 오른쪽 트리의 값은 부모 노드보다 커야하는 특징이 있습니다.
이진 탐색. 트리는 트리의 높이에 영향을 받아 높이 h일때 시간 복잡도가 O(h) 입니다.
트리의 균형이 한쪽으로 치우쳐진 경우 worst case가 되고 O(n)의 시간 복잡도를 가집니다.
이런 worst case를 막기 위해 나온 기법이 RBT(Red - Black Tree) 입니다.
RBT(Red - Black Tree)
RBT는 BST를 기반으로 하는 트리 형식 자료구조이며,
BST의 삽입, 삭제 연산 과정에서 발생할 수 있는 문제를 해결하기 위해 만들어졌습니다.
BST의 특징을 모두 가지고 있으며, 노드의 child가 없는 경우 child가 가리키는 포인터는 NIL 값을 지정합니다.
이러한 NIL들을 Leaf node로 간주하며, 모든 노드를 빨간색 또는 검은색으로 색칠하며, 연결된 노드들은 색이 중복되지 않습니다.


