[Python] 파이썬의 순열과 조합 알고리즘

파이썬 라이브러리

순열과 조합의 경우 파이썬 내부의 라이브러리를 사용하면 직접 구현하는것 보다 훨씬 빠른 속도로 구현할 수 있다.

알고리즘 문제의 경우 빠른 속도를 요구하므로, 순열과 조합의 라이브러리를 꼭 숙지해야 한다.

 

순열과 조합은 매우 비슷해서 구분이 어렵고 헷갈리기 때문에 차이를 알고 구별할 수 있도록 학습한다.

 

파이썬에서는 itertools를 사용해서 순열과 조합을 구현할 수있다.

 

from itertools import permutations

https://docs.python.org/ko/3/library/itertools.html

itertools — Functions creating iterators for efficient looping

 

 순열 ( permutations)

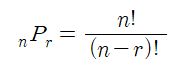
순열은 길이가 N인 반복 가능한 객체에 대하여 중복을 허용하지 않고 r개를 뽑아서 나열한다.

중복을 허용하지 않기 때문에 순서대로 나열하며, 순서에 의미가 있다.

같은 값이 뽑히더라도 순서가 다르면 다른 경우의 수로 취급하며, 조합보다 많은 경우의 수를 가지게 된다.

 

예를 들어서 [a,b,c] 리스트에서 2(r)개의 순열을 뽑을 경우의 수는 아래와 같다.

[ab, ac, bc, ba, ca, cb]

ab와 ba는 다른 경우로 인정하므로, 총 6가지의 경우의 수가 나온다.

 

permutations 함수를 사용할 경우 아래와 같이 표현할 수 있다.

permutations(반복 가능한 객체, r(순열 수 ))로 나타낸다.

from itertools import permutations
data_set = ['a','b','c']
for i in permutations(data_set, 2):
    print(i, end=" ")

 

('a', 'b') ('a', 'c') ('b', 'a') ('b', 'c') ('c', 'a') ('c', 'b') 

위와 같은 결과를 얻을 수 있으며, 문자열로 출력을 원할 경우 list로 변경 후 .join을 사용한다.

 

for i in permutations(data_set, 2):
    print("".join(i),end=" ")

 

조합 (combinations)

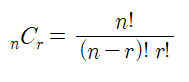
조합은 길이가 N인 반복 가능한 객체에 대해서 중복을 허용하지 않고 r개를 뽑는 경우의 수를 확인한다.

뽑는 경우의 수만을 보기 때문에 뽑는 순서를 고려하지 않는 특징을 가지고 있다.

 

combinations 함수를 사용할 경우 아래와 같이 표현할 수 있다.

combinations(반복 가능한 객체, r(조합 수 ))로 나타낸다.

 

from itertools import combinations
data_set = ['a','b','c']
for i in combinations(data_set, 2):
    print("".join(i),end=" ")

 

ab ac bc

문자열로 출력했기 때문에 위와 같은 결과를 얻을 수 있다.

 

 중복 순열 (permutaton with repetition)

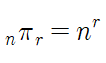
중복 순열은 순열과 다르게 중복을 허용한다.

중복을 혀용하므로, 순열의 3*2*1... 의 방식이 아닌 3*3*3.. 의 방식으로 순열을 구한다.

[a,b,c] 배열로 3자리 문자열을 만들 경우 [a,b,c] * [a,b,c] * [a,b,c] 총 27가지의 데이터가 생성 된다.

 

파이썬에서 중복 순열은 product 라이브러리 함수를 사용한다.

from itertools import product

 

중복 순열은 product(리스트 1, 리스트 2, 리스트 3,,,,)와 같은 방식으로 사용한다.

결과 값을 9개씩 출력하기 위해서 index가 9로 나눠지는 경우 줄 바꿈을 적용했다.

from itertools import product
for idx,i in enumerate(product(['a','b','c'],['a','b','c'],['a','b','c'])):
    if (idx%9==0): print()
    print(i, end=" ")

 

('a', 'a', 'a') ('a', 'a', 'b') ('a', 'a', 'c') ('a', 'b', 'a') ('a', 'b', 'b') ('a', 'b', 'c') ('a', 'c', 'a') ('a', 'c', 'b') ('a', 'c', 'c') 
('b', 'a', 'a') ('b', 'a', 'b') ('b', 'a', 'c') ('b', 'b', 'a') ('b', 'b', 'b') ('b', 'b', 'c') ('b', 'c', 'a') ('b', 'c', 'b') ('b', 'c', 'c') 
('c', 'a', 'a') ('c', 'a', 'b') ('c', 'a', 'c') ('c', 'b', 'a') ('c', 'b', 'b') ('c', 'b', 'c') ('c', 'c', 'a') ('c', 'c', 'b') ('c', 'c', 'c')

 

위와 같은 결과를 얻을 수 있으며, 3*3*3 총 27개의 결과를 얻을 수 있다.

 

중복 조합(combination with repetition)

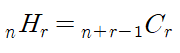
중복 조합은 조합과 다르게 값을 중복해서 사용한다.

중복 가능한 n개의 순서를 생각하지 않고 r개를 선택하는 경우의 수를 생각한다.

순서를 생각하지 않기 때문에 중복 순열과는 다른 결과를 반환한다.

[a,b,c] 배열로 3자리 문자열을 만들 경우 순서를 바꾸면 같은 경우를 제외하고 조합을 생성한다.

 

3가지 문자 중에서 3개의 대표 숫자를 순서를 생각하지 않고 뽑는 경우의 수를 생각하면 된다.

파이썬에서 중복 조합은 combination with repetition 라이브러리 함수를 사용한다.

 

from itertools import combinations_with_replacement
for idx,i in enumerate(combinations_with_replacement(['a','b','c'],3)):
    print(i, end=" ")

 

('a', 'a', 'a') ('a', 'a', 'b') ('a', 'a', 'c') ('a', 'b', 'b') ('a', 'b', 'c') ('a', 'c', 'c') ('b', 'b', 'b') ('b', 'b', 'c') ('b', 'c', 'c') ('c', 'c', 'c')

위와 같은 결과를 얻을 수 있으며, 3가지 문자 중에서 3가지 조합을 추출했으므로, 결과 값이 적다.

 

 

 라이브러리 사용 후기 

 

순열, 조합의 라이브러리를 직접 구현하는 경우와 라이브러리를 사용하는 경우의

테스트 시간을 비교해보았더니 대략 8-10배 정도의 실행 속도 차이를 보였다.

 

실제 코딩 테스트를 진행할 때는 자동완성 기능을 사용할 수 없는 경우가 있기 때문에

함수 사용법을 정확하게 숙지하고, 각 함수가 필요한 경우를 이해하고 있어야겠다.