에라토스테네스의 체
소수를 찾을 때 가장 적은 시간 복잡도를 소요하는 알고리즘이다.
여러 개의 수가 소수인지 아닌지를 판별하며, N보다 작거나 같은 모든 소수를 찾을 때 사용할 수 있다.
에라토스테네스보다 시간 복잡도가 높은 알고리즘과 비교하여 해당 알고리즘의 이점을 파악한다.
일반적인 소수 찾기 알고리즘
소수의 판별법을 사용한다.
소수란 2보다 큰 자연수 중에서 1과 자기 자신을 제외한 자연수로는 나누어 떨어지지 않는 자연수이다.
6의 경우 1,2,3,5을 약수를 가지므로 소수가 아니고, 7의 경우 1,7만을 약수로 가지므로 소수라고 할 수 있다.
가장 간단한 소수 판별법은 아래와 같으며, 어떤 수의 소수를 찾을 때 시간 복잡도가 O(n)이 된다.
# 가장 간단한 소수 판별법
# 모든 수를 나누어서 소수를 구함
def is_prime_number(n):
# 2부터 n -1 까지 모든 수를 확인
for i in range(2,n):
# n이 해당 수로 나누어 떨어지는 지 확인
if n % i == 0:
return False
return True
print(is_prime_number(6))
print(is_prime_number(7))
n이 10의 5승만 되더라도 수가 무수히 커지므로, 위의 방식은 비효율적인 알고리즘이라고 할 수 있다.
개선 된 알고리즘 : 제곱근 찾기
위의 알고리즘을 계선하기 위해서 규칙을 찾는다.
16을 예로 들을 경우 다음과 같은 규칙을 찾을 수 있다.
1. 1 * 16
2. 2 * 8
3. 4 * 4
4. 8 * 2
5. 16 * 1
소수를 찾는 알고리즘에서 가운데 약수를 기준으로 각 등식이 대칭적인 형태를 가진다.
즉, 가운데 약수까지만 확인한다면 알고리즘의 시간 복잡도를 크게 줄일 수 있다.
n개의 수 리스트에서 중앙 값의 가운데 약수를 찾으려면 n의 루트 값을 찾으면 된다.
# 제곱근을 활용한 약수 탐색
import math
def is_prime_number(n):
for i in range(2, int(math.sqrt(n))+1):
# n이 해당 수로 나누어 떨어지는 지 확인
if n % i ==0:
return False
return True
기존에 n개의 수를 탐색했다면, 이제는 루트 n의 수를 탐색하면 된다.
즉 O(n)의 시간 복잡도에서 O(루트(n))의 시간 복잡도로 줄일 수 있다.
하지만 여전히 n의 수가 무한히 커질 경우 큰 시간복잡도를 가지게 된다.
개선 된 알고리즘 : 에라토스테네스의 체
소수를 판별하기 위해서 에라토스테네스의 체를 사용한다.
1. 2부터 n까지의 모든 자연수를 나열한다.
2. 남은 수 중에서 아직 처리하지 않은 가장 작은 수 i를 찾는다.
3. 남은 수 중에서 i의 배수를 모두 제거한다.
4. 더 이상 반복할 수 없을 때까지 2,3번 반복한다.
에라토스테네스의 체는 위의 과정을 거치는 알고리즘이다.
배수를 소거하는 방법을 사용하며, 이 방법으로 남은 배열이 소수의 리스트가 된다.
적은 수부터 배수를 차례로 소거했기 때문에 매우 빠른 알고리즘이며 NloglogN의 시간복잡도를 가진다.
이 알고리즘을 사용하면 O(루트(n))의 시간 복잡도에서 O(NloglogN)의 시간 복잡도까지 감소시킬 수 있다.
예를 들어서 2부터 16까지의 수를 에라토스테네스의 체 알고리즘을 적용한다.
[ 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 ]
처리하지 않은 가장 작은 수는 2이므로 2를 제외한 2의 배수를 모두 제외한다.
[ 2, 3, /, 5, /, 7, /, 9, /, 11, /, 13, /, 15, / ]
남은 수 중에 처리하지 않은 가장 작은 수는 3이므로 3을 제외한 3의 배수를 모두 제외한다.
[ 2, 3, /, 5, /, 7, /, /, /, 11, /, 13, /, /, / ]
남은 수 중에 처리하지 않은 가장 작은 수는 5이므로 5를 제외한 5의 배수를 모두 제외한다.
[ 2, 3, /, 5, /, 7, /, /, /, 11, /, 13, /, /, / ]
... 이와 같은 과정을 반복하며 남은 수는 모두 소수가 된다.
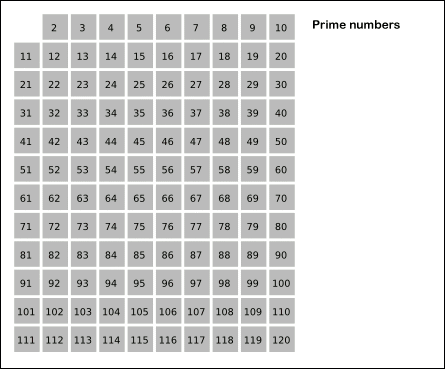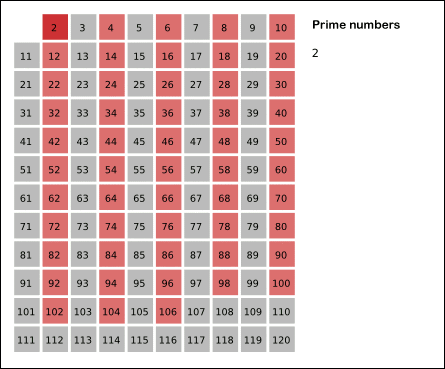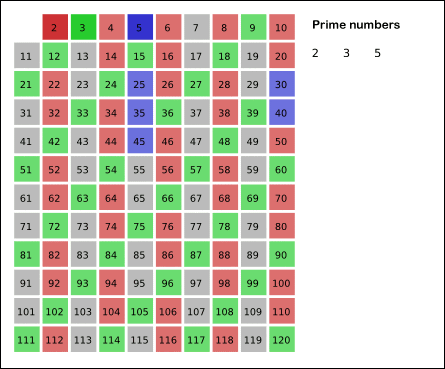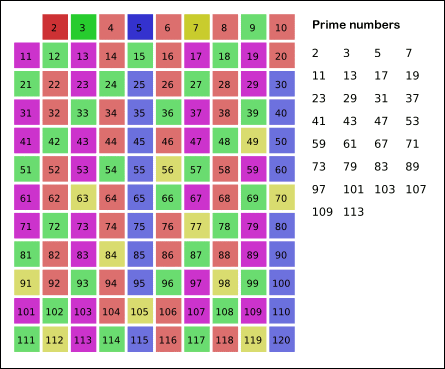
코드로 에라토스테네스의 체 구현
매 단계마다 남은 수 중에서 아직 처리하지 않은 작은 수를 찾으며,
위의 개선된 두 알고리즘을 모두 사용하여, N의 제곱근 까지만 해당 과정을 반복한다.
# 에라토스테네스의 체 활용
import math
n = 1000
array = [True for i in range(n+1)]
# 알고리즘 구현
for i in range(2,int(math.sqrt(n))+ 1):
if array[i] == True: # 가까운 소수 발견
# 해당 소수를 제외한 모든 배수 제거
j = 2
while i * j <= n:
array[i*j] = False #소수가 아닌 수 제거
j += 1
for i in range(2,n+1):
if array[i]:
print(i,end=" ")
에라토스테네스의 체 알고리즘을 사용할 경우, 선형 시간 알고리즘과 비슷한 효과를 얻을 수 있다.
해당 알고리즘으로 문제 풀이
문제 출처
https://swexpertacademy.com/main/code/problem/problemDetail.do?contestProbId=AXWXH_h695kDFAST
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
SW 아카데미의 제곱수 만들기 : 10965번 문제를 이 알고리즘을 적용시켜서 풀었다.
어떤 수와의 제곱근 관계를 구해야 하는데, 제곱근을 나누면 소수의 곱이 된다.
즉 홀수 만큼의 소수의 곱을 가지며, 홀수 만큼의 소수의 곱 * B를 만족하는
자연수 B를 구하면 정답이 된다.
에라토스테네스의 체 알고리즘을 통해서 소수의 집합을 구한 뒤, 홀수로 된 소수의 곱을 찾아서
나머지 한 수를 구하면 정답이 된다.
# 10 * 7 의 제곱근 까지 구해야함
# 제곱근 이상의 수 중 소수로 더 이상 나눌 수 없으면 소수
# 에라토스테네스의 체 알고리즘 사용
# 이미 제곱수라면 결과는 1
# 제곱수가 아닌 경우 동일한 소수로 나누는 횟수가 홀수인 경우
# 해당 소수를 곱하면 제곱 수가 됨
# -> 제곱수는 소수의 곱으로 이루어짐
# -> 횟수가 홀수인 경우 A를 곱했을 때 제곱수가 됨
from math import sqrt
max_n = int(sqrt(10**7))
array = [True for _ in range(max_n+1)]
for i in range(2, int(max_n**0.5) + 1):
if array[i]:
# 에라토스테네스의 체 사용
# 해당 수가 소수가 아니라면 그 수의 곱도 소수가 아님
j = 2
while i * j <= max_n:
array[i * j] = False
j +=1
# 소수 리스트
prime = []
for i in range(2,len(array)):
if array[i]:
prime.append(i)
result = []
for t in range(int(input())):
n = int(input())
answer = 1
if sqrt(n) != int(sqrt(n)): #이미 배수인지 확인
for p in prime:
count = 0
while n% p == 0:
n//=p
count+=1
if count % 2 != 0: # 홀수 확인
answer *=p
if n == 1 or p > n:
break
if n>1:
answer *= n
result.append(answer)
for i in range(len(result)):
print(f"#{i+1} {result[i]}")

